TeamNet: A Collaborative Inference Framework on the Edge

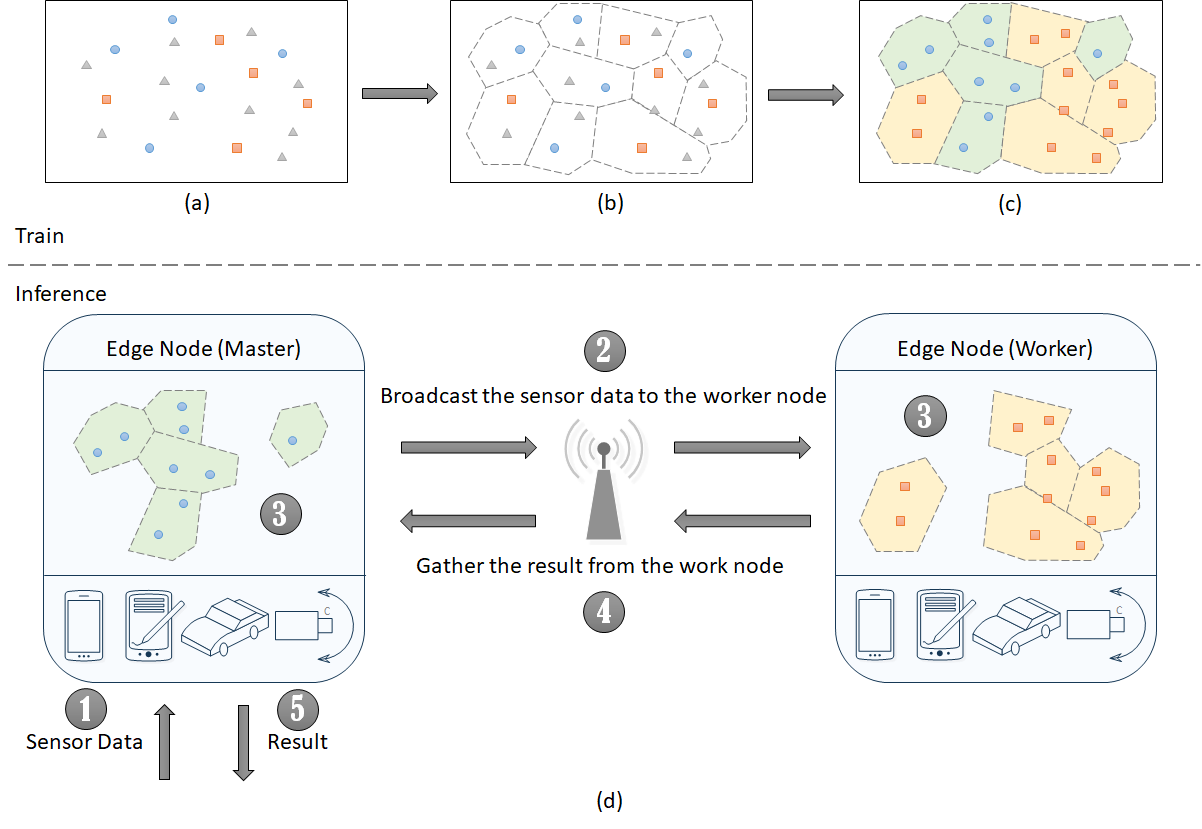
With significant increases in wireless link capacity, edge devices are more connected than ever, which makes possible forming artificial neural network (ANN) federations on the connected edge devices. Partition is the key to the success of distributed ANN inference while unsolved because of the unclear knowledge representation in most of the ANN models. We propose a novel partition approach (TeamNet) based on the psychologically-plausible competitive and selective learning schemes while evaluating its performance carefully with thorough comparisons to other existing distributed machine learning approaches.

TeamNet’s training and inference can be illustrated on two edge nodes. At the training stage: (a) Initially, each expert has very limited knowledge about the dataset but each is randomly more certain of some data than the others. (e.g. One expert is more certain of the square data points, while the other expert is more certain of the circle data points. However, neither of them has knowledge of the triangle data points.) (b) With this preference, it is more likely for each expert to select the more certain data to learn, respectively. (c) Gradually, with the help of gradient descent, each expert has learned its more certain data from the entire dataset.

At the inference stage: (d) Each expert is deployed to one edge node. (Step 1) When one edge node, called the master, receives the sensor data, (Step 2) it broadcasts the data to the other edge node, called the worker. (Step 3) Both then perform inference in parallel. (Step 4) At the time the inference completes, the master gathers the result (with uncertainty) from the worker. (Step 5) Then the master compares its uncertainty with the worker’s, and select the one with the least uncertainty as the final result. It is necessary to collaborate with the worker since neither of them is trained with all data.

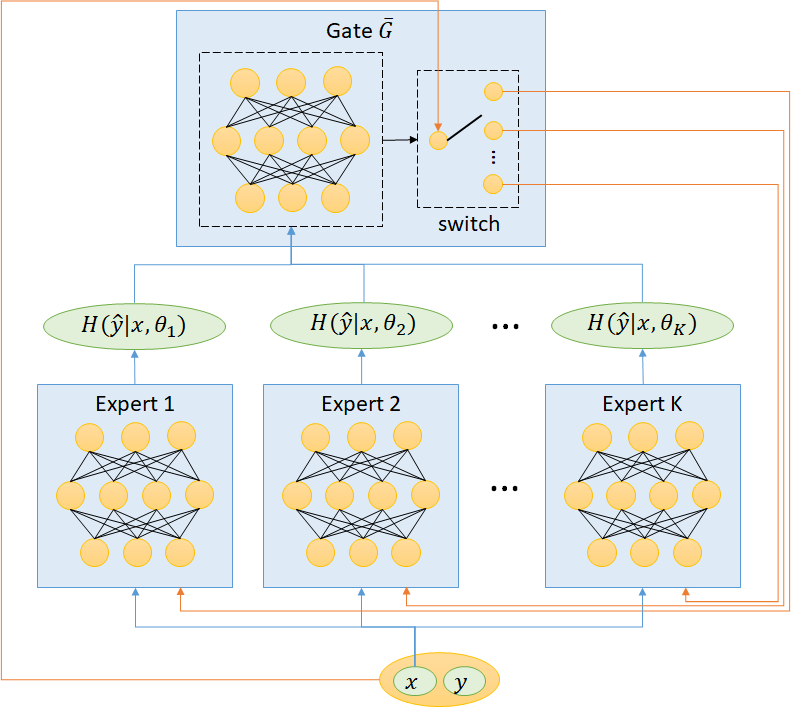
The key challenge is the “richer gets richer” phenomenon. A more knowledgeable expert is generally more certain of more data examples, as naturally in the human society. Specifically, regardless of how the expert models are initialized, they are predisposed to biases and fall into the “richer gets richer” phenomenon. To solve this problem, a gate (judge) must be introduced to decide which data example should be assigned to which expert to learn, and such a decision should be based on the uncertainty estimation of all experts for the particular data example.

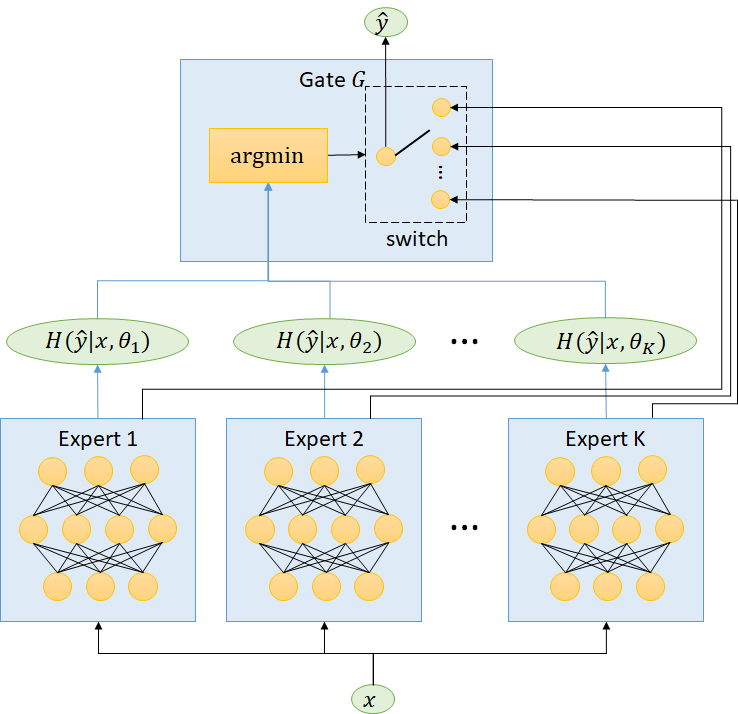
In training, a) The primary objective is to divide the input data \(𝐷\) into \(𝐾\) partitions \(𝐷_1,𝐷_2,...,𝐷_𝐾\) such that for any \((𝑥, 𝑦) \in 𝐷_𝑖\), Expert \(𝑖\) can predict the correct label \(𝑦\) and has the least predictive entropy for \(𝑥\) among all experts with high likelihood. b) The secondary objective is to have \(|𝐷_𝑖 | \approx {|𝐷| \over 𝐾}, 𝑖=1, 2, ...,𝐾.\) The reason why having the second objective is to tackle the "richer gets richer" phenomenon.

Formally speaking, consider \(K\) experts, each modeled as a function \(𝑓(𝑥;𝜃_𝑖)\) , parameterized by \(𝜃_𝑖, 𝑖=1, 2, ...,𝐾\). Let \(𝑝(\hat{𝑦}=𝑐|𝑥, 𝜃_𝑖)\) be the predictive probability of output \(𝑐\) for input \(𝑥\) from Expert \(𝑖\). The predictive entropy of Expert \(𝑖\) of input \(𝑥\) is defined as, \[𝐻(𝑦 ̂│𝑥,𝜃_𝑖 )=−∑_𝑐 𝑝(\hat{𝑦}=𝑐│𝑥,𝜃_𝑖 ) \log⁡ 𝑝(\hat{𝑦}=𝑐|𝑥,𝜃_𝑖)\] The predictive entropy of a model reflects its “uncertainty” of a data instance drawn from the same distribution of the training data.

The gate function \(\bar{𝐺}\) splits the current batch into \(𝐾\) partitions for training. We define \(\bar{𝐺}\) as: \[\bar{𝐺}(𝑥,\delta)={\arg\min}_𝑖⁡ \delta_𝑖 \cdot 𝐻(𝑦 ̂|𝑥,𝜃_𝑖)\] where \(\mathbf{\delta}=(\delta_1, \delta_2,...,\delta_𝐾)\) are control variables to be determined. When experts are biased, direct application of the argmin gate would result in unevenly split data. It is important to update \(\bar{𝐺}\) dynamically based on some measure of the biases of the experts.

Let \(𝐺(𝑥)={\arg\min}_𝑖 𝐻(\hat{𝑦}|𝑥, 𝜃_𝑖)\) denote the index of the Expert which is least uncertain of the input \(𝑥\). Given the current batch \(\beta\) and \(\mathbf{\delta}\), let \[\gamma_i = \frac{\sum_{x\in \beta}{\unicode{x1D7D9}_{G(x)=i}}}{|\beta|},\] be the percentage of data examples that are assigned to Expert \(𝑖\) by \(𝐺\), and \[\bar{\gamma}_i(\mathbf{\delta}) = \frac{\sum_{x\in \beta}{\unicode{x1D7D9}_{\bar{G}(x,\mathbf{\delta})=i}}}{|\beta|}, i = 1, 2,\ldots, K, \] be the percentage of the data examples that are assigned to Expert \(𝑖\) by the dynamic gate \(\bar{𝐺}\).

Under the assumption that the data in \(\beta\) is balanced, the bias in Expert \(𝑖\) can then be characterized by \(\gamma_𝑖−{1 \over 𝐾}\). by adjusting \(\mathbf{\delta}\), we can "correct" the biases by assigning more data to the expert who would have received less training data according to gate \(𝐺\) \[\min_{\mathbf{\delta}}{\sum_{i=1}^{K}\left|\bar{\gamma}_i(\mathbf{\delta}) - \left( \frac{1}{K} - a\cdot (\gamma_i - \frac{1}{K})\right)\right|}, \] where \(𝑎\) is a hyperparameter in \((0,1)\).

As the experts become less biased, \(\bar{𝐺}\) approaches an argmin gate, where the training example is given to the model with the least uncertainty. At the inference stage, it is sufficient to have the argmin function to determine which expert is least uncertain of the given data input. TeamNet’s inference time is generally faster than other mixture of experts (MoE) approaches since argmin gate is much simpler.

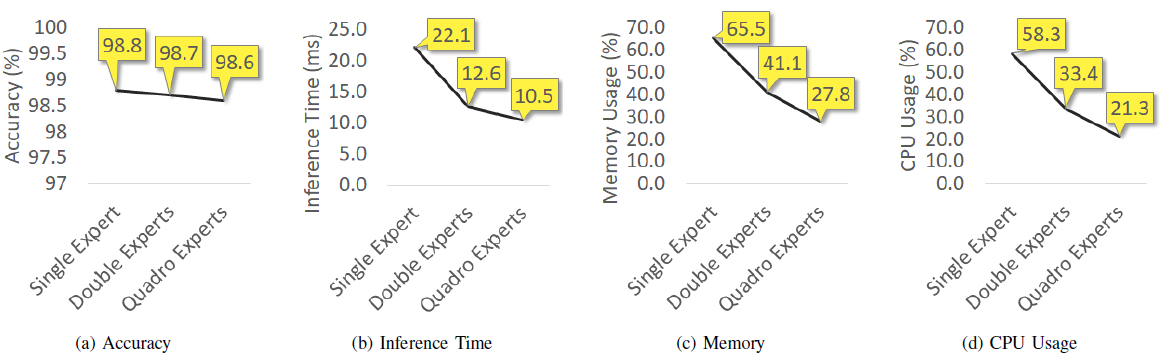
TeamNet’s performance is evaluated on Raspberry Pi 3 Model B+ for handwritten digit recognition. The MNIST dataset is used where there are 10 classes grey-color handwritten digits from digit zero to nine. With more experts in TeamNet, (a) The accuracy is generally not compromised. (b) inference becomes faster, And (c,d) memory and CPU consumption become smaller on the edge node.

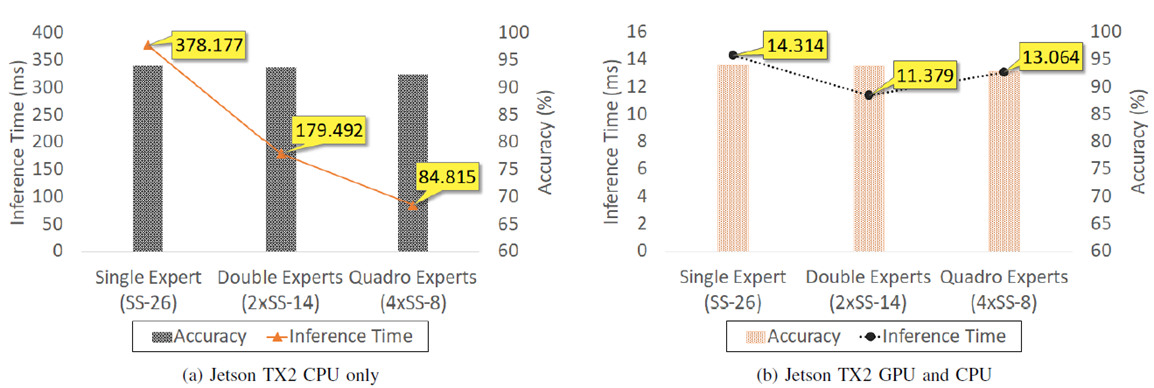
In another experiment, TeamNet’s performance is evaluated on Jetson for image classification. CIFAR-10 is a benchmark dataset in image classification. There are 10 classes in the dataset such as the airplanes, automobiles, birds, and dogs. It consists of 60000 32-by-32 color images, with 50000 images for training and 10000 images set aside for evaluation. (a) On Jetson CPUs, inference becomes faster with more experts in TeamNet, while accuracy is generally not compromised. (b) On Jetson GPUs, the fastest inference is achieved when there are two experts in TeamNet. Because there is a fixed communication cost over the WiFi network, a shorter time cannot be achieved when the communication latency is too close to the actual latency caused by the computation unless the model size is significantly larger and more computation is needed.

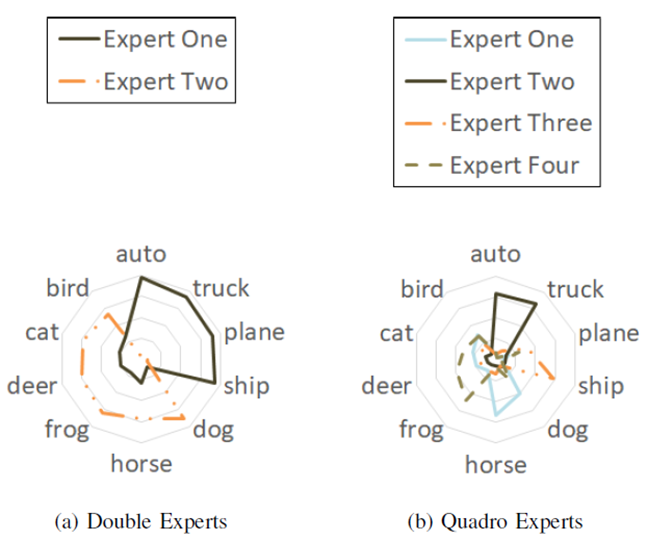
Specialization is emphasized in TeamNet. (a) With two experts being trained in TeamNet, one of the experts is more certain of machines such as airplanes, automobiles and trucks, while the other one is more certain of animals such as cats and dogs. (b) With four experts being trained in TeamNet, two of them are more certain of animals, while the other two are more certain of machines.

TeamNet is a novel framework for collaborative inference among storage-and-compute-limited edge devices. Unlike existing computation-partition solutions that take a pre-trained model and determine the best partitions between edge devices and the cloud, TeamNet is a model partition approach by training multiple small specialized models. TeamNet is proven to work well with the commonly used neural networks (CNNs and MLPs). Experiments have demonstrated that TeamNet can be executed on low-end edge devices such as Raspberry Pi and Jetson TX2 devices.